Введение

Актуальность. По данным Всемирной организации здравоохранения (ВОЗ), ежегодно в результате дорожно-транспортных происшествий гибнет около 1,3 млн чел., при этом дорожно-транспортный травматизм является ведущей причиной смертности среди детей и молодых людей в возрасте от 5 до 29 лет.

Несмотря на достигнутые в последние десятилетия успехи в хирургии печени, летальность при её повреждении остаётся высокой, особенно в случае закрытой травмы. Организация помощи пострадавшим с сочетанной травмой является одной из актуальных проблем экстренной хирургии. Лечение данной категории больных представляет трудную и далеко не решённую задачу. Послеоперационная летальность при травме печени остаётся по-прежнему высокой. Травма живота остается одной из наиболее актуальных проблем неотложной хирургии [Yu et al., 2016; Duron et al., 2020; Ordonez et al., 2020; Coccolini et al., 2023]. Одним из сложных в техническом отношении вопросов гемостаза является остановка паренхиматозного кровотечения [Одишелашвили и др., 2021, Гаврищук и др., 2022, Подолужный и др., 2023].

Для остановки кровотечений из ран печени предложено много способов гемостаза. Основным оперативным методом является ушивание ран. Недостатками всех швов, накладываемых при ранении печени, является появление зон некроза между швами. При больших по площади поверхностных повреждениях используют различные методы коагуляционных устройств (диатермокоагуляция, лазерная коагуляция, аргоноплазменная коагуляция). Все эти методы коагуляции дают нестабильный гемостатический результат, часто расширяют зону некроза в ране [Евтихов, 2020; Маскин, 2020]. В крупных хирургических клиниках проводят эмболизацию печеночных артерий. Главными недостатками этого способа являются его высокая стоимость и отсутствие такого оборудования в городских и районных больницах [Iida et al., 2020].

В условиях обычных клиник для гемостаза при ранениях печени все шире применяются варианты тампонирования раны, например, сальником, различными гемостатическими средствами (губки, порошки, пленки). При этом остаются проблемы биоинертности, наличия местных и системных реакций [Воронцов и др., 2020; Маскин, 2020; Ротькин, 2023; Iida et al., 2020; Ordonez et al., 2020; Vorontsov et al., 2021].

Основной причиной неблагоприятного исхода травм печени является внутрибрюшное кровотечение, поэтому своевременность оперативного вмешательства и выбор адекватного способа гемостаза имеют особое значение [Воронцов и др., 2020; Умедов и др., 2023; Ordonez et al., 2020; Vorontsov et al., 2021]. Несмотря на все современные достижения в области практической медицины, хирургические вмешательства при травмах печени до сих пор остаются основным методом лечения [Ordonez et al., 2020]. Часто при обработке ран печени используют методы физического воздействия, биологические ткани или синтетические материалы, что обусловливает развитие комплекса структурно-функциональных изменений в органе [Маскин, 2020; Vorontsov et al., 2021]. Это наглядно видно в зоне раневого дефекта, определяющего особенности течения репаративных процессов. Морфологическая картина повреждений при различных видах лечения влияет на сроки заживления, а зачастую и на его эффективность [Воронцов и др., 2020; Vorontsov et al., 2021]. Очевидно, что клинико-морфологические сопоставления играют одну из самых важных ролей при разработке новых методик хирургических вмешательств.

При оперативных вмешательствах при травме печени возникает иногда необходимость повторных оперативных вмешательств ввиду наличия геморрагического отделяемого по дренажу, желчеистечения. Для понимания хирургу более точного объема повреждения паренхимы печени и внутрипеченочных структур (вены, артерии, желчные протоки) необходима более точная диагностика в предоперационном периоде. Исходя из вышесказанного, мы предлагаем создание математической модели, которая позволяет более точно описать повреждения при травматических воздействиях на печень.

В связи с этим проблема оценки картины повреждений остается актуальной и требует дальнейшего изучения. Данное исследование является первым этапом разработки прогностической математической модели оценки повреждения печени у пациентов с травматическим повреждением этого органа. Модель основывается на данных предоперационного КТ исследования и интраоперационной картине травмы печени. Численное моделирование позволяет оценить истинный объём повреждения паренхимы печени, что позволит оперирующему хирургу удалить все повреждённые ткани.

Цель. Оценка влияния сегментирования модели печени на распределение механических напряжений при моделировании ударного воздействия методом конечных элементов.

Материалы и методы

В исследовании приняли участие 9 пациентов с травматическими повреждениями печени. Нами был проведен анализ медицинских карт стационарных пациентов, госпитализированных в Брянскую городскую больницу № 1 с травматическим повреждением печени, которые были верифицированы по КТ органов брюшной полости. Оперированы в экстренном порядке. Анализ проведен на основании медицинской документации.

Исследование проведено на базе Государственного автономного учреждения здравоохранения «Брянская городская больница № 1», города Брянска. Набор пациентов выполнялся в период с 01.12.2019 до 31.06.2023, пациенты выписаны из стационара в удовлетворительном состоянии. Продолжительность периода наблюдения за послеоперационным периодом одного пациента не менее 8 месяцев.

Критерии включения. Пациенты обоих полов, от 18 лет и старше, подписание информированного согласия на участие в клиническом исследовании, госпитализированы в экстренном порядке c травматическим повреждением печени, оперированы в экстренном порядке, наличие выполнения КТ исследования в приёмном покое, травма печени была сопоставима, отсутствие сочетанной травмы, пациенты без сопутствующей патологии печени.

Критерии невключения. Пациенты с тяжелой сочетанной травмой, пациенты по шкале ASA 4-5, AAST 5, пациенты, которым на этапе обследования не было выполнено КТ органов брюшной полости, пациенты с установленной сопутствующей патологией печени, пациенты младше 18 лет, пациенты с сочетанной травмой.

Критерии исключения. Отказ от участия в клиническом исследовании, пациенты, умершие в послеоперационном периоде.

Описание критериев соответствия

Диагностические критерии. Учитывали клинико-демографические параметры: пол, возраст, механизм травмы, соматическую коморбидность (установленный диагноз «цирроз печени» или «гепатоз печени», «фиброз печени» в соответствии с критериями, утвержденными в клинических рекомендациях «цирроз и фиброз печени» (2021 г.), министерством здравоохранения Российской Федерации).

Морфологические критерии. Были отобраны пациенты с анатомическими параметрами печени, соответствующими геометрическим параметрам модели, имевшейся в распоряжении авторов. По КТ были определены характерные размеры, показанные на рис. 1:
A – длина правой доли, B – толщина правой доли, С – длина левой доли, D – толщина левой доли (таблица 1). Отклонения размеров, использованных в модели, от средних значений, определенных по КТ, не превышает 3σ для всех измерений, кроме C. Поскольку предполагалось моделирование удара, нанесенного по правой доле, значительное отклонение размера C от среднего не учитывалось.

Подбор участников в группы

Подбор участников в группы не предусмотрен. Группа наблюдения 9 пациентов была сформирована из общего числа пациентов (n = 94) с изолированным травматическим повреждением печени, обратившихся в центр за медицинской помощью в период с декабря 2019 г. по июнь 2023 г. Основным показателем исследования является оценка эффективности моделирования с учетом деления на сегменты и без разделения. Дополнительные показатели исследования не предусмотрены.

Предикторы

Исследование направлено на создание математической модели, которая помогает хирургу определить тактику и объем оперативного вмешательства при травматических повреждениях печени. Модель позволяет определить объем повреждающего травматического воздействия на паренхиму печени, смоделировать границы резекции поврежденной ткани печени и понять объем оперативного вмешательства.

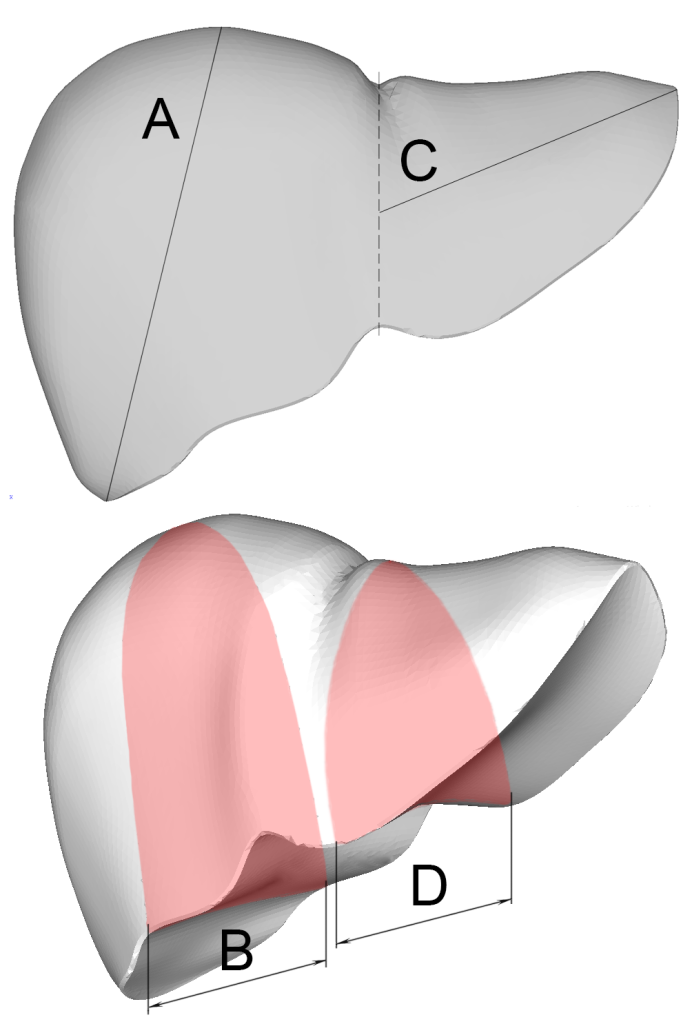
Рис. 1. Характерные размеры печени для определения соответствия органа модели
Fig. 1. Morphometric parameters of the liver for organ-model comparison

Таблица 1
Table 1

Характерные размеры печени (мм)
Characteristic dimensions of the liver (mm)

Для численного моделирования ударного воздействия на печень использован метод конечных элементов – численный метод решения дифференциальных уравнений с частными производными. Метод широко используется для решения задач механики деформируемого тела. В этих задачах решением задачи являются перемещения точек исследуемого объекта, по которым затем вычисляются механические напряжения в каждой из этих точек.

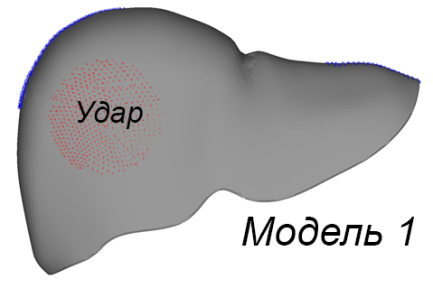
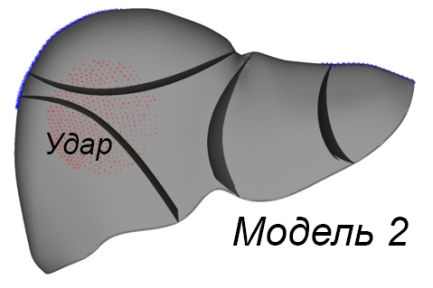
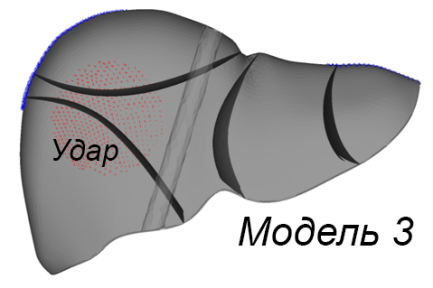
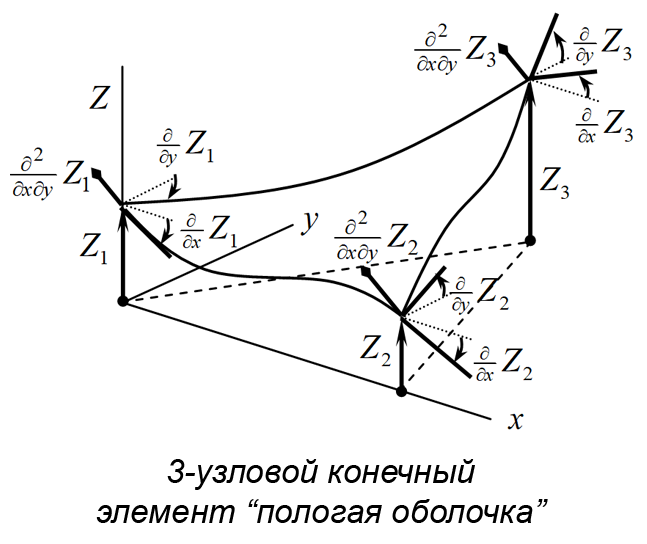
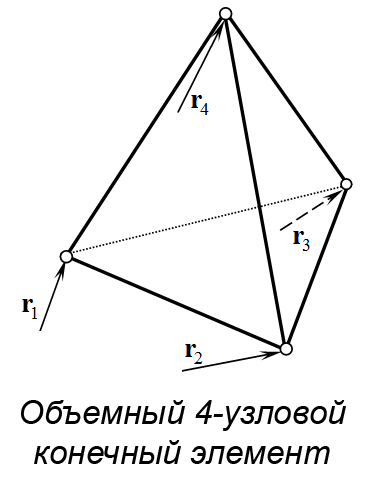
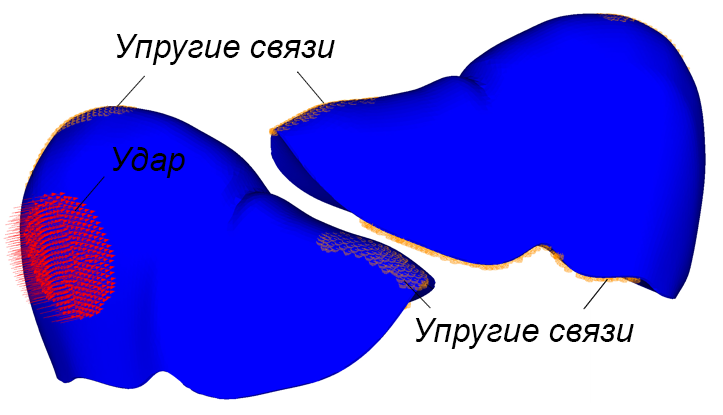
Были разработаны три расчетные модели (рис. 2а). Первая модель включает паренхиму печени без внутренних структурных разделений. Вторая модель поделена на пять сегментов перегородками толщиной 1 мм, имеющими форму поверхностей второго порядка. Третья модель аналогична второй, но дополнительно включает воротную вену, представленную полым цилиндром диаметром 10 мм с толщиной стенки 1 мм. Расчетные модели построены на основе графической модели органа путем автоматизированной дискретизации последней на конечные элементы двух типов. Паренхима представлена объемными линейными изопараметрическими 4-узловыми элементами; перегородки между сегментами печени смоделированы 3-узловыми элементами типа пологая оболочка Кирхгофа (рис. 2b). В литературе описываются анизотропные механические свойства ткани печени, полученные экспериментально [Umale et al., 2013; Karimi et al., 2018]. Параметрами модели являются модуль упругости E, модуль сдвига G, коэффициент Пуассона µ и плотность ρ ткани паренхимы печени и перегородок, разделяющих ее на доли. В работе Karimi et al. отмечено существенное различие параметров упругости тканей печени при растяжении и сжатии (E = 12.16 ± 1.20 кПа при осевом растяжении и E = 196.54 ± 13.15 кПа при осевом сжатии) и их нелинейная зависимость от величины деформации. В модели использовано максимальное значение модуля упругости E = 200 кПа для материала паренхимы и вдвое большее значение для материала границ сегментов. Поскольку основной целью данного исследования является оценка влияния сегментирования модели печени на распределение напряжений при ударе, а не моделирование конкретного случая удара по конкретному органу, точный учет параметров материала не является критически значимым на текущем этапе работы. По той же причине в расчетах использована линейная упругая модель изотропного материала, таким образом,. Tamura et al. в работе [Tamura et al., 2002] приводят экспериментальную оценку предела прочности ткани печени в пределах от 127,1 до 192,7 кПа при скорости нагружения 5 мм/с. Механические свойства материала приведены в табл. 2. Внешние связи наложены в виде упругих закреплений в местах прикрепления печени к диафрагме и переходным складкам по боковым поверхностям (рисунок 2c). Ударная нагрузка приложена кинематически. Для этого на наружной боковой поверхности печени точкам круглой области диаметром 60 мм сообщены переменные во времени перемещения, направленные внутрь печени.

Таблица 2
Table 2

Механические свойства материала
Mechanical properties of material

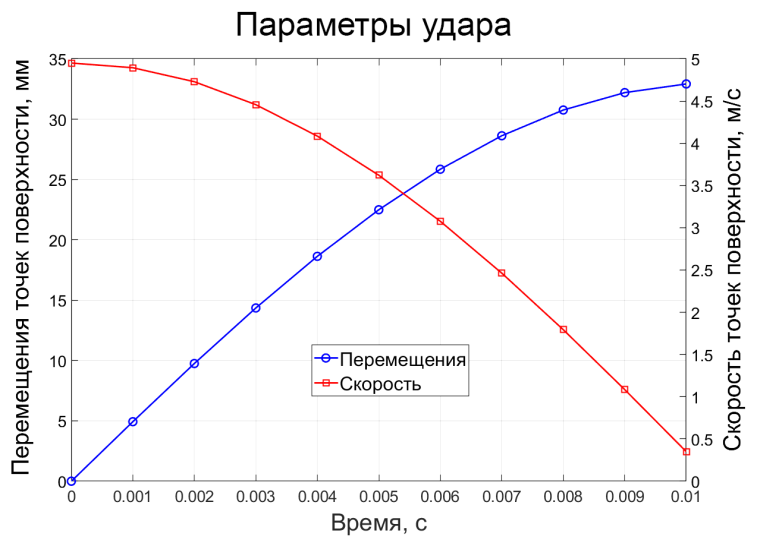
Перемещения и скорости точек во времени описываются функциями z(t) = 33∙sin(150t) и v(t) = 4950∙cos(150t) соответственно. Начальная скорость точек поверхности удара составляет 4,95 м/с, максимальное перемещение – 32,9 мм. Графики изменения перемещений точек поверхности и их скорости во времени показаны на рисунке 2d.

a)

b)

c)

d)

Рис. 2. Три модели печени (a); использованные типы конечных элементов (b); схема наложения внешних связей и приложения нагрузок (c); параметры удара (d)
Fig. 2. Liver model geometries (a); finite element types employed (b); constraints and load application schema (c); impact simulation parameters (d)

На всех этапах решения задачи использовался программный комплекс DSMFEM, разработанный при участии одного из авторов. Комплекс является универсальным и используется в различных инженерных областях, примеры его применения представлены в работах [Ольшевский, 2019; Olshevskiy et al., 2018].

Результаты

В исследовании приняли участие 9 пациентов, поступивших в порядке скорой помощи в хирургический стационар ГАУЗ Брянская городская больница № 1 с диагнозом травматическое повреждение печени. Пациенты находились на стационарном лечении от 7 до 16 суток с последующим послеоперационным периодом наблюдения каждого пациента 8 месяцев.

Характеристика групп участников

Из 9 пациентов 7 пациентов мужского пола (77,8 %) и 2 пациента женского пола, что составило 22,2 %. Средний возраст пациентов – 32 года. Средний возраст пациентов мужского пола – 26,1 года, женского пола – 42,5 года. По механизму травмы пациенты, доставленные с места ДТП, – 6 пациентов (66,5 %), кататравма – 2 пациента (22,3 %) и 1 пациент с бытовой травмой (11,2 %). Все пациенты доставлены в стационар в порядке скорой помощи.

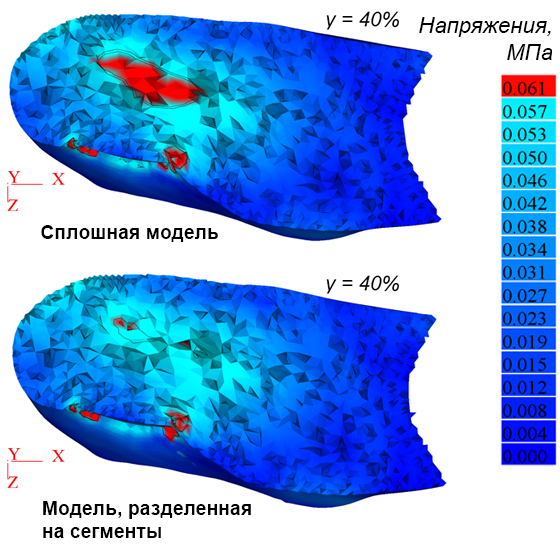
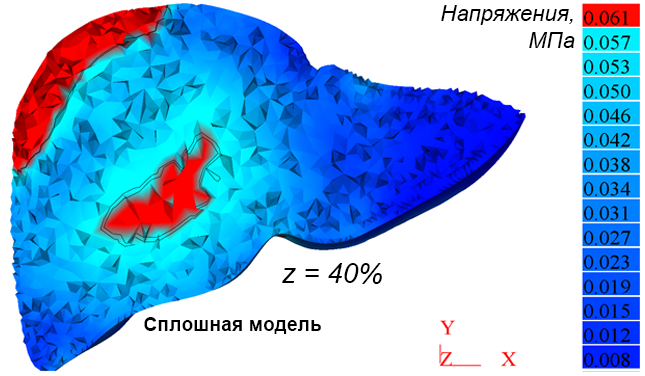
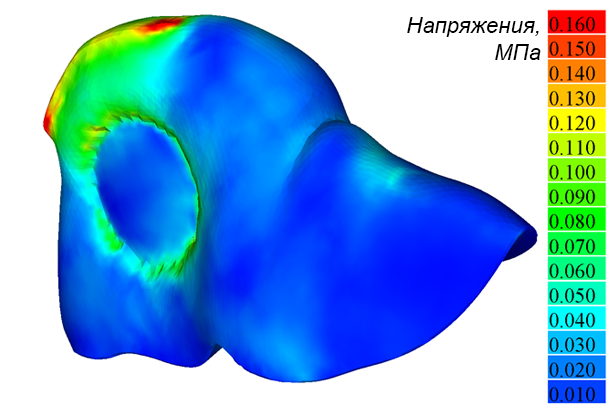
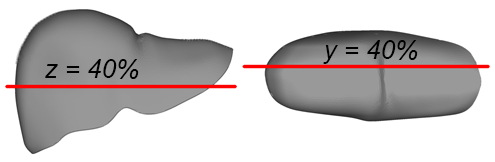
Рис. 3а иллюстрирует деформацию печени и общую картину распределения напряжений IV теории прочности (Мизеса) на поверхности печени в момент времени t = 9 мс. Разработанный инструментарий позволяет визуализировать распределение напряжений в сечениях печени, параллельных плоскостям координат. Схема построения таких сечений для случая, рассматриваемого здесь, показана на рисунке 3b. На рисунке 3c приведены распределения напряжений в горизонтальном сечении печени на расстоянии от начала координат в направлении оси y, равном 40 % от наибольшего размера печени для сплошной и разделенной на сегменты моделей. Аналогичные распределения напряжений во фронтальном сечении на расстоянии 40 % от начала координат вдоль оси z показаны для тех же моделей на рисунках 3d и 3e соответственно. Красным цветом выделены области, в которых эквивалентные напряжения σ_э  60 кПа. Конфигурация этих областей существенно различается в зависимости от учета разделения модели на сегменты.

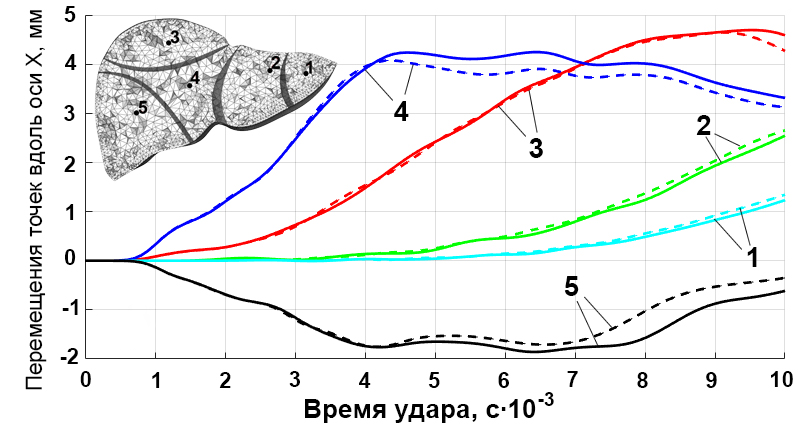
Еще одним способом оценки влияния разделения модели на сегменты может служить исследование перемещений характерных точек модели, выбранных в пределах каждого из сегментов, во время удара. На рисунке 3f показано расположение точек 1–5, перемещения которых оценивались, и графики перемещения этих точек вдоль оси x во времени. При отсутствии в модели разделения на сегменты все точки оказываются в едином изотропном пространстве (сплошные линии на рисунке 3f), тогда как при наличии такого разделения каждая точка находится внутри отдельного сегмента (пунктирные линии на рисунке 3f). Различие в перемещениях, перпендикулярных направлению удара, наиболее выражено для точек 3 и 5 (свыше 1 мм), возрастает с ходом времени и присутствует даже для наиболее удаленной от места удара точки 1.

c)

d)

e)

f)

Рис. 3. Эквивалентные напряжения (Мизеса) на поверхности модели печени (а); схема построения сечений (b); напряжения в избранном горизонтальном сечении для сплошной и разделенной на сегменты (c) моделей; напряжения в избранном фронтальном сечении для сплошной (d) и разделенной на сегменты (e) моделей; перемещения точек 1–5 во времени при ударе (f)

Fig. 3. Von Mises stress distributions on the liver model surface (a); cross-sections positions (b); stresses in a selected horizontal plane for solid  and segmented (c) liver models; stresses in a selected frontal cross-section for intact (d) and segmented (e) liver models; displacement of points 1–5 over time during impact (f)

Следует отметить, что сравнение напряжений и перемещений было проведено лишь для одного произвольного направления удара и может быть более выраженным в других случаях, поскольку диапазоны скоростей, направлений, точек приложения и других параметров удара могут быть весьма широкими. Следовательно, учет разделения печени на сегменты имеет принципиальное значение при анализе картины повреждений ткани этого органа при ударе, что следует иметь в виду при разработке моделей, используемых для расчетной оценки ударного воздействия.

Обсуждение

Ограничения исследования

Основным ограничением исследования являются то, что математическая модель органа была построена на основе усредненного графического представления печени человека, а не по натурным данным, и является идеализированной в геометрическом отношении. Модель существует в единственном варианте и не предусматривает изменений формы за счет настройки каких-либо параметров. Это было сделано намеренно, поскольку цель работы состояла в первичной оценке влияния разделения модели печени на доли на распределение механических напряжений, а не в моделировании реального клинического случая. Построение модели на основе КТ реального органа привело бы к ее значительному усложнению, а анатомические особенности геометрии затруднили бы идентификацию эффектов, которые обусловлены учетом перегородок при моделировании ударного воздействия. Заметим, что методы построения математических моделей органов по результатам КТ описаны в литературе, и авторы планируют использовать их в дальнейшей работе. Существенную погрешность в результаты моделирования вносит используемая в работе линейная упругая модель материала, которая не учитывает анизотропные свойства тканей печени. Для решения поставленных в исследовании задач такое упрощение является приемлемым, однако в ходе уточнения математической модели органа потребуется отказ от него в пользу анизотропного материала.

Вторым ограничением является недостаток данных об ударных воздействиях: их направлении, скорости, свойствах материала тела, с которым произошло соударение. В реальных клинических случаях хирургу приходится иметь дело с последствиями таких соударений, в то время как характеристики удара могут быть восстановлены лишь приблизительно. Это положение вещей можно частично преодолеть, смоделировав большое количество соударений с разными параметрами, и получить объем данных, который позволит сопоставлять картины распределения напряжений в органе с характеристиками ударов.

Третье ограничение касается проверки адекватности моделирования удара путем сопоставления распределения повреждающих напряжений с реальной картиной внутренних повреждений печени и связано с тем, что в большинстве случаев при поступлении пациента с травмой в приемное отделение КТ исследование не проводится и данные для сопоставления отсутствуют.

Интерпретация

При помощи математического моделирования было показано, что наличие в модели перегородок оказывает влияние на картину распределения механических напряжений. Отчетливо наблюдаются зоны с уровнем повреждающих напряжений, которые различны для моделей с перегородками и без них при одинаковом внешнем ударном воздействии. Подробное изучение особенностей влияния наличия перегородок, соотнесение их с анатомическими особенностями органов разных пациентов и создание методики для использования результатов в клинической практике является весьма трудоемкой задачей, которая выходит за рамки данной работы, являющейся первым шагом в этом направлении. Тем не менее авторы полагают, что задачи, которые были поставлены перед исследованием, были выполнены.

Значение

Потенциальное клиническое использование модели заключается в разработке программно-аппаратного комплекса, способного выполнять прямое моделирование внутренних повреждений печени при поступлении пациента с травмой в приемное отделение. Комплекс состоит из мобильного или стационарного персонального компьютера сравнительно небольшой мощности, на котором установлено специализированное приложение для моделирования повреждений печени от внешнего воздействия. Действия хирурга при этом сводятся к следующему. Наблюдая картину наружных повреждений при осмотре пациента и имея примерное представление о механизме получения травмы с его слов или со слов сотрудников скорой помощи, данных предоперационного исследования КТ, хирург формирует исходные данные для расчета: выбирает из прилагаемой библиотеки модель печени, указывает на модели область нанесения удара, задает примерный диапазон его возможных направлений и скоростей и запускает расчет, который длится несколько минут. При необходимости возможно выполнение нескольких вариантов расчета. Результат расчета представляет собой трехмерную карту повреждений, построенную на основе распределения повреждающих напряжений в модели органа. Эти сведения позволяют хирургу планировать операцию, снижают ее травматичность и риски для пациента.

Численному моделированию травм печени посвящено значительное количество исследований [Cai et al., 2016; Pellicer-Valero et al., 2020, Bustamante et al., 2024]. В работе Umale et al.  описана трехмерная модель печени, включающая систему вен, но не содержащая разделения органа на сегменты. Основной задачей авторов работы была разработка методики построения конечно-элементной модели печени по данным компьютерной томографии. Результатом стала трехмерная гомогенная модель, материал которой имеет вязкоупругие свойства. В качестве примера использования модели рассмотрено напряженно-деформированное состояние печени под действием внешнего давления.

Значительная часть исследований рассматривает модели внутренних органов, включая печень, в составе вычислительной модели туловища при моделировании автомобильных крэш-тестов и баллистических испытаний. Так, в работе Cai et al. трехмерная гомогенная модель печени использована в составе полной модели тела человека для моделирования крэш-теста и бокового удара в грудь [Cai et al., 2016]. Трехмерная модель, включающая внутренние органы, кости, мышцы и кожу, была построена Степановым и др. на основе данных КТ среднестатического мужчины и используется для исследования характера заброневой контузионной травмы [Степанов и др., 2018]. Моделирование внутренней структуры органов для этих задач не требуется, поэтому они представлены однородными средами. Наиболее совершенной является трехмерная математическая модель печени, построенная по данным томографии [Pellicer-Valero et al., 2020]. Комбинация метода конечных элементов и машинного обучения сделала возможным высокоточное моделирование механического воздействия на печень. В модели присутствует система желчевыводящих протоков, однако нет разделения печени на сегменты, а также не учитываются вязко-упругие свойства материала тканей паренхимы в предположении, что моделируемое воздействие является достаточно медленным, а не ударным. Таким образом, описанные в литературе математические модели печени обладают свойствами и возможностями, которые соответствуют задачам исследований, поставленных их авторами.

Предлагаемая авторами данной статьи модель служит для расчета распределения механических напряжений в печени при ударе и принципиально отличается от моделей, упомянутых выше, наличием разделения на секторы перегородками, механические свойства которых отличаются от свойств ткани паренхимы. Модель также включает воротную вену, представленную полым цилиндром. Таким образом, модель не является гомогенной структурой и отражает принципиальные морфологические особенности печени. Учет внутреннего строения органа существенно влияет на распределение механических напряжений в его ткани во время удара, а следовательно, и на расчетную картину повреждений тканей по сравнению со случаем, когда рассматривается гомогенная модель. Результаты получаются прямым моделированием удара с использованием метода конечных элементов, широко распространенным в решении задач механики деформируемого тела. Предлагаемая методика позволяет произвольно задавать направление и скорость удара, а также форму области, воспринимающей удар, что дает возможность моделировать произвольный спектр реальных травмирующих воздействий.

Заключение

Построенная математическая модель печени с системой секторов существенно отличается от сплошной гомогенной модели. Поскольку реальный орган – в данном случае печень – является системой функциональных единиц (разделена на систему секторов), то при численном моделировании авторы рекомендуют использовать модель с разделением. Это позволит более эффективно применять полученные результаты расчетов в оценке клинической картины после травмы и ее последующем лечении.